A syllogism is a kind of logical argument that applies deductive reasoning to arrive at a conclusion based on two or more propositions that are asserted or assumed to be true. 

---

Formula's For Syllogisms

Types of Statements 

The four basic statements in syllogism are, 

• All As are B (Eg. All Mobiles are cameras) 
• Some As are B (Eg. Some cats are dogs) 
• No A is B (Eg. No rabbit is a pig) 
• Some As are not B (Eg. Some cats are not humans) 

These statements can be classified into two categories as shown in below table. 

Alternate Words 

Basic Diagrams 

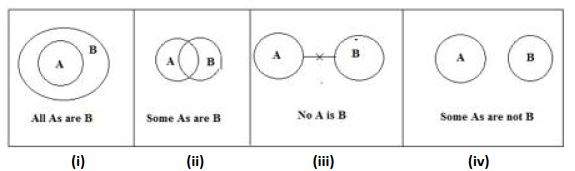
For (i) statement, i.e. All As are B,        

Circle  A    should  be  inside   B   or   A  and    B can   be   equal.   But circle A should not exceed B. 

For (ii) statement, i.e. Some As are B,

Circle A and B should be connected always. It should not separate. 

For (iii) statement, i.e. No A is B,

We should not connect circle A and circle B.  

For (iv) statement, i.e. Some As are not B,

We can connect circle A and circle B. 

Complementary pair 

In the Complementary pair, subject and predicate should be same in both the conclusions. If one conclusion is true, definitely the other conclusion will be false and vice versa. There are two complementary pairs in syllogism. 

Pair I : All As are B & Some As are not B 

If “All As are B” is true, definitely “Some As are not B” is false. If “Some As are not B” is true, definitely “All As are B” is false. 

Pair II: No A is B & Some As are B 

If “No A is B” is true, definitely “Some As are B” is false. If “Some  As  are B” is true, definitely “No A is B” is false. 

Procedure: 

Step 1: Draw the basic diagram for the given statements. 

Step 2a: If all are positive conclusions, Check those conclusions in basic diagram and decide which one is true or false. Don’t draw any other diagram if all are positive in conclusion. 

Step 2b: If there is negative conclusion and it is true in basic diagram, try to make it false by drawing its complementary pair. While drawing alternate diagram, it should not violate any other given statements. If you are able to draw alternate diagram, without violating any statement. Then the negative statement is false. 

Examples: (Positive Conclusions) 

Q.1. Statements 

1. All grapes are apples                      

2. All apples are mangoes  

Conclusions 

1. All grapes are mangoes 

2. All mangoes are grapes 

3. Some grapes are mangoes 

Answer: (1) and (3) are   true 

---

Examples (Negative Conclusion)  

Q.1. Statements 

1. All months are weeks 

2. Some week are days 

Conclusions 

1. No month is day 

2. Some weeks are months 

Answer : (2) is true 

---