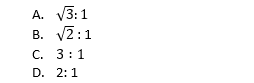Practice Question For Geometry
1) Two angles are supplementary and the ratio of the angels is 1:4. what is the value of smaller angle?
- 36 degrees
- 45 degrees
- 35 degrees
- 72 degrees
Answer: A
Explanation:
As we know that the angles are supplementary so sum of angles will be 180 degree.
Let us assume that the ratio factor is r.
According to question,
Angles are supplementary and have a ratio of 1:4.
r + 4r = 180
5r = 180
r = 180/5
r = 36
2) The complement of 30°20′ is:
- 69°40′
- 59°40′
- 35°80′
- 159°40′
Answer: B
Explanation:
complement of 30°20′ = 90° – ( 30°20′ ) = 90° – ( 30° + 20′ )
= (89° – 30°) + (1° – 20′)
= 59° + 60′ – 20′ [ ∴ 1° = 60°′]
= 59° + 40′ = 59°40′.
3) In the given, AB || CD. Then X is equal to:
- 93°
- 103°
- 89°
- 285°
Answer: D
Explanation:
Through O, draw a line l parallel to both AB and CD. Then
∠1 = 45° (alt. ∠S)
and ∠2 = 30° (alt. ∠S)
∴ ∠BOC = ∠1 + ∠2 = 45° + 30° = 75°
So, X = 360° – ∠BOC = 360° – 75° = 285°
Hence X = 285°.
4) An angle is equal to one-third of its supplement. Its measure is equal to:
- 40°
- 50°
- 45°
- 55°
Answer: C
Explanation:

5) In the adjoining figure, AB || CD, t is the traversal, EG and FG are the bisectors of ∠BEE and ∠DFE respectively, then ∠EGF is equal to:
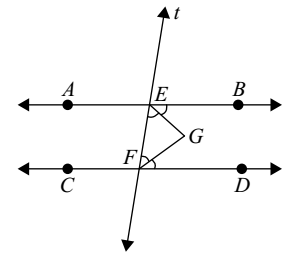
- 90°
- 75°
- 80°
- 110°
Answer: A
Explanation:
AB || CD and t transversal intersects them at E and F
∠BEF + ∠EFD = 180° (co-interior angles)
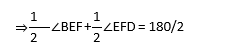
∠FEG + ∠EFG = 90°
In Δ GEF
∠EGF + ∠FEG + ∠EFG = 180°
∠EGF + 90° = 180°
∠EGF = 90°.
The above result can be restated as:
If two parallel lines are cut by a traversal, then the bisectors of the interior angles on the same side of the traversal intersect each other at right angles.
6) Find the measure of an angle, if six times its complement is 12° less than twice its supplement :
- 48°
- 96°
- 24°
- 58°
Answer: A
Explanation:
Let, the measure of the required angled be A°.
Then, measure of its complement = ( 90 – A )° measure of its supplement = (180 – A)°
According to question,
6(90° – A) = 2(180° – A) –12°
12° – 6A = 360° – 2A – 12°
4A = 192°
A = 48°.
7) In fig., AB || CD, ∠a is equal to:
- 93°
- 103°
- 83°
- 97°
Answer: A
Explanation:
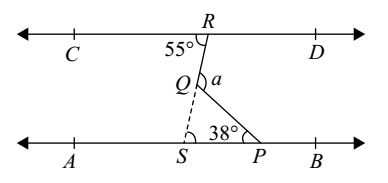
CD || AB (Given)
Produce RQ to meet AB in S
∠CRS = ∠PSR (at. int. ∠s)
But ∠CRS = 55°
∠PSR = 55°
Now in QSP
∠QSP + ∠QPS + ∠PQS = 180°
55° + 38° + ∠SQP = 180°
∠SQP = 180° – 93° = 87°
But angle a and ∠PQS are linear
∠a = 180° – 87°
∠a = 93°
8) In the following figure, ∠B : ∠C = 2 : 3, find ∠B + ∠C.
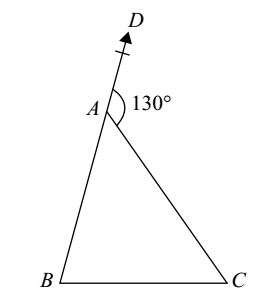
- 120°
- 52°
- 78°
- 130°
Answer: D
Explanation:
∠DAC = ∠B + ∠C
(Exterior angle prop. of a Δ ABC)
According to question,
130° = 2A + 3A
5A = 130°
A = 26°
∠B = 52°; ∠C = 78°
9) In a ΔABC, if 2∠A = 3∠B = 6∠C, Then ∠A is equal to:
- 60°
- 30°
- 90°
- 120°
Answer: C
Explanation:
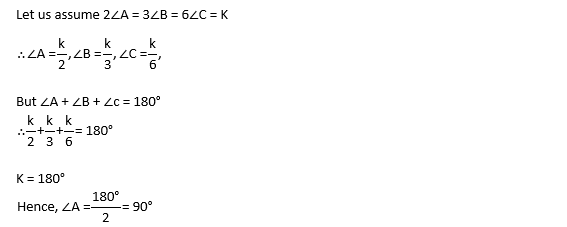
10) A, B, C are the three angles of a Δ. If A − B = 15° and B − C = 30°. Then ∠A is equal to :
- 65°
- 80°
- 75°
- 85°
Answer: B
Explanation:
Since A, B and C are the angles of a Δ,
∴ A + B + C = 180° ...... (1)
According to question,
A – B = 15°
A = B + 15°...... (2)
B – C = 30°;
B = C + 30° ....... (3)
ut the value of B from equation (2) in Equation (1), we will get
∴ A = B + 15°
A = C + 30° + 15°
A = C + 45° ......... (4)
From the equation,
∴ A + B + C = 180°
(C + 45°) + (C + 30°) + C = 180°
3C + 45° + 30° = 180°
3C = 180° – 75° = 105°
C = 35° ........ (5)
From equation (4)
A = C + 45°
Put the value of C from equation (5), we will get
∠A = 35° + 45° = 80°.
11) In a right angled Δ ABC, Right angled at A, AD ⊥ BC. Then:
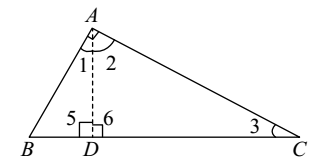
A. AD2 = BD * CD
B. AD2 = AB* AC
C. AD2 = BD * AB
D. AD2 = CD* AC
Explanation:
From above given right angle triangle, we can see that
Since ∠1 + ∠2 = ∠2 + ∠3 (Each 90°)
∴ ∠1 = ∠3 [Each 90°]
Also ∠5 = ∠6 [Each 90°]
∴ ΔADB ∼ ΔCDA [AA Similarity]
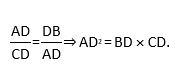
12) In center of a triangle lies in the interior of :
- An isosceles triangle only
- Any triangle
- An equilateral triangle only
- A right triangle only
Answer: B
Explanation:
We know that in center of every triangle (acute, obtuse and right angle) lies in its interior.
Hence required answer will be any triangle.
13) If the sides of a right triangle are x, x + 1 and x – 1, then the hypotenuse:
- 5
- 4
- 1
- 0
Answer: A
Explanation:
From given figure, we have
Let, (x + 1) be the hypotenuse and perpendicular = x - 1, base = x.
By Pythagoras theorem,
∴ (x + 1)
2 = x
2 + (x + 1)
2 ⇒ x = 4
∴ Hypotenuse = 4 + 1 = 5.
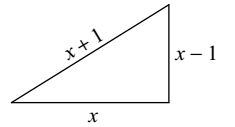
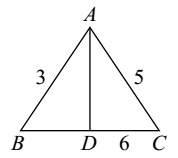
14) In a triangle ABC, the length of the sides AB, AC and BC are 3, 5 and 6 cm respectively. If a point D on BC is drawn such that the line AD bisects the angle A internally, then what is the length of BD?
- 2 cm
- 2.25 cm
- 2.5 cm
- 3 cm
Answer: B
Explanation:
In a triangle ABC,
Given :- AB = 3 cm , AC = 5 cm and BC = 6 cm
We know that BD : DC = AB : AC
BD : DC = 3 : 5
∴ Divided BC = 6 in the ratio 3 : 5
BC = 3x + 5x = 6 ⇒ 8x = 6 ⇒ x = 6/8 = 0.75
BD = 2.25, CD = 3.75.
15) The number of tangents that can be drawn to two non-intersecting circles:
- 4
- 3
- 2
- 12
Answer: A
Explanation:
We know that when two circle neither touch nor intersect and one lies outside the other, then 4 common tangents can be drawn.
For 4 common tangents, we get
∴ r1 + r2 < c1c2
Hence, The number of tangents = 4
16) In Δ ABC, the median BE intersects AC at E, if BG = 6 cm, where G is the centroid, then BE is equal to:
- 7 cm
- 9 cm
- 8 cm
- 10 cm
Answer: B
Explanation:
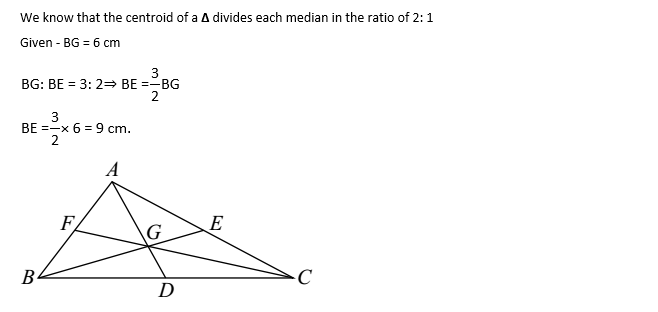
17) If the sides of a triangle are produced then the sum of the exterior angles i.e., ∠ a + ∠ b + ∠ c is equal to:
- 180°
- 90°
- 360°
- 270°
Answer: C
Explanation:
From above figure,
Since every exterior angle is equal to sum of interior opposite angles,
So, ∠ a = A + B, ∠ b = B + C and ∠ c = A + C
We know that, A + B + C = 180°
∠a +∠b + ∠c = 2(A + B + C) = 2 × 180° = 360°.
18) In the given figure, side BC of Δ ABC is produced to form ray BD and CE || BA. Then ∠ ACD is equal to:
- ∠A - ∠B
 (∠A + ∠B)
(∠A + ∠B)- ∠A + ∠B
 (∠A - ∠B)
(∠A - ∠B)
Answer: C
Explanation:
From above given figure, we can see that
CE || BA and AC is the transversal.
∴ ∠4 = ∠1 (alternate interior ∠s) .......... ( 1 )
Again, CE || BA , BD is the transversal.
∴ ∠5 = ∠2 (corresponding ∠s) ................( 2 )
Adding equations ( 1 ) and ( 2 )
∴ ∠4 + ∠5 = ∠1 + ∠2
∴∠ACD = ∠A + ∠B.
19) In fig, AB = AC, D is a point on AC and E on AB such that AD = ED = EC = BC. Then ∠A : ∠B.
- 1 : 2
- 2 : 1
- 3 : 1
- 1 : 3
Answer: D
Explanation:
As per given figure , we can see that
In ΔBCE, BC = EC, ∴ ∠B = ∠BEC
In ΔCDE, ED = EC, ∴ ∠ECD = ∠EDC
and In ΔADE, AD = ED, ∴ ∠AED = ∠A
Now ∠B = ∠BEC = ∠A + ∠ECD = ∠A + ∠EDC = ∠A + ∠EAD + ∠AED
{ ∴ ∠EDC = ∠EAD + ∠AED }
=∠A + ∠A + ∠A = 3∠A { By ASA property }
∠A : ∠B = 1 : 3.
20) The two sides of a right triangle containing the right-angle measure 3 cm and 4 cm. The radius of the incircle of the triangle is?
- 3.5 cm
- 1.75 cm
- 1 cm
- 0.875 cm
Answer: C
Explanation:
If the incircle of a triangle ABC touches BC at D, then |BC - CD| = |AB - AC|
In our case, AC = 5, AB = 3
AC – AB = 2
CD – BD = 2
In our case, BC = 4
BD + BD = 4 and – BD + DC = 22
CD = 3
BD = 1 = OE = Radius of the in circle.
21) If one of the diagonals of a rhombus is equal to its side, then the diagonals of the rhombus are in the ratio?
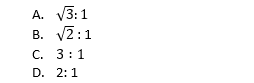
Answer: B
Explanation:
Let ABCD is a rhombus in which AB = BC = CD = DA = diagonal CA.
In triangle ABC ,
AB = BC = CA , therefore ∠B = 60°
D = ∠B = 60°
A=180 - ∠B = 180° - 60° =120°
C = ∠A=120°
Hence, The ratio of diagonals = √2 : 1
22) Two circles of unit radius touch each other and each of them touches internally a circle of radius two, as shown in the following figure. The radius of the circle which touches all the three circles:
Answer: C
Explanation:
From given figure , we can see that
CC1 = 1, OC1 = 1 + r
OC = AC – AO = CD – AO = 2 – r [ AC and CD are the radii of the bigger circle ]
(OC1)2 = (CC1)2 + (OC)2
(1 + r)2 = 12 + (2 - r)2
1 + r2 + 2r = 1 + 4 + r2 - 4r ⇒ 2r + 4r = 4 ⇒ 6r = 4
r = 2 / 3
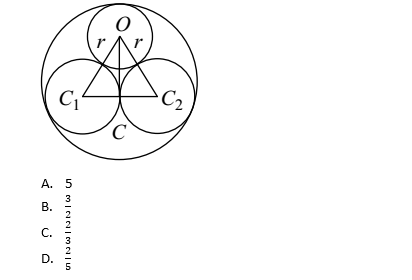
23) If, in the following figure, PA = 8 cm, PD = 4 cm, CD equal to 3 cm, then AB is?
- 3 cm
- 3.5 cm
- 4 cm
- 4.5 cm
Answer: D
Explanation:
From above given figure, we have
PA = 8 cm, PD = 4 cm and CD = 3 cm, PC = PD + CD = 4 + 3 = 7 cm
we know that, PA X PB = PC X PD
8 x PB = 7 x 4 ⇒ 2 x PB = 7
PB = 3.5 cm
So, AB = PA – PB = 8 – 3.5 = 4.5 cm
24) In a triangle ABC, ∠A = x°, ∠B = y° and ∠C = (y + 20)°. If 4x – y = 10, then the triangle is?
- Right-angled
- Obtuse-angled
- Equilateral
- None of these
Answer: A
Explanation:
Given:- ∠A = x° , ∠B = y° , ∠C = ( y + 20 )° and 4x – y = 10
We know that, ∠A + ∠B + ∠C = 180°
x + y + ( y + 20 ) = 180°
x + 2y = 180 - 20 = 160° ........... i
4x – y = 10 ........... ii
From i and ii, we get
y = 70, x = 20\
The angles of the triangle are 20° , 70° , 90° .
Hence, the triangle will be Right-angle triangle.
25) Of all the chords of a circle passing through a given point in it, the smallest is that which:
- Is trisected at the point
- Is bisected at the point
- Passes through the centre
- None of these
Answer: D
Explanation:
Let C(O, r) is a circle and let M is a point within it where O is the centre and r is the radius of the circle.
Let CD is another chord passes through point M.
We have to prove that AB < CD.
Now join OM and draw OL perpendicular to CD.
In right angle triangle OLM,
OM is the hypotenuse.So OM > OL
chord CD is nearer to O in comparison to AB.
CD > AB
AB < CD
So, all chords of a circle of a circle at a given point within it, the smallest is one which is bisected at that point.
Hence required answer will be option D.



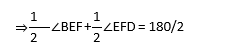


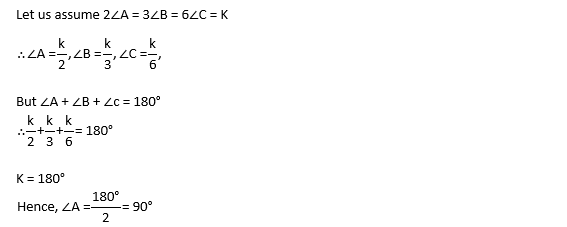

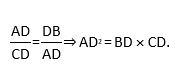



 (∠A + ∠B)
(∠A + ∠B)