Practice Question For Progressions
1. The 7th term of an AP is -39/12 and the 15th term is -103/12. What is the 27th term?
A. -187/12
B. -191/12
C. -199/12
D. -205/12
Answer: C
Explanation:
The 7th term is a + 6d = -39/12
The 15th term is a + 14d = -103/12
Equating these terms with their values and solving as simultaneous equations, we get a = 3/4 and
d = – 2/3.
So, the 27th term is (a + 26d) = 3/4 + (-52/3) = -199/12.
2. In an AP of 21 terms, the sum of the first 3 terms is – 33 and that of the middle 3 is 75. What is the sum of the AP?
A. -955
B. -1155
C. 525
D. 715
Answer: C
Explanation:
The AP can be expressed as a, (a + d), ---, (a +20d).
The sum of the first 3 terms is (3a + 3d) = -33 and the sum of the middle 3 terms is (3a + 30d) = 75. Solving these two equations,
we get a = -15 and d = 4.
The sum of the 1st 21 terms is (21/2) (2 * -15 + 20 * 4) = 525.
3. The 6th term of an AP is 6 and the 16th term is 14. What is the 27th term?
A. 106/5
B. 22/5
C. 118/5
D. 114/5
Answer: D
Explanation:
The 6th term is a + 5d = 6
The 16th term is a + 15d = 14
Equating these terms with their values and solving as simultaneous equations,
we get a = 2 and d = 4/5.
So the 27th term is (a + 26d) = 2 + (104/5) = 114/5.
4. In an AP, the ratio of the 2nd term to the 7th term is 1/3. If the 5th term is 11, what is the 15th term?
A. 28
B. 31
C. 33
D. 36
Answer: B
Explanation:
The 2nd and the 7th terms are (a + d) and (a + 6d) respectively.
The ratio of these terms is 1/3.
Solving this ratio, we get 2a = 3d.
The 5th term is (a + 4d) = 11.
Substituting for a, we get a = 3 and d = 2.
Therefore, the 15th term is (a + 14d) = 31.
5. The sum of the first 3 terms in an AP is 6 and that of the last 3 is 16. If the AP has 13 terms, what is the sum of the middle three terms?
A. 7
B. 9
C. 11
D. 13
Answer: C
Explanation:
The AP can be expressed as a, (a + d), ---, (a +12d).
The sum of the first 3 terms is (3a + 3d) = 6 and that of the last 3 is (3a + 33d) = 16.
Solving these equations, we get a = 5/3 and d = 1/3.
The sum of the middle 3 terms is (3a + 18d) = 11.
6. In an AP, the ratio of the 7th term to the 10th term is -1. If the 16th term is -15, what is the 3rd term?
A. 11
B. 13
C. -11
D. -13
Answer: A
Explanation:
The 7th and the 10th terms are (a + 6d) and (a + 9d) respectively.
The ratio of these terms is -1.
Solving this ratio, we get -2a = 15d. The 16th term is (a + 15d) = -15.
Substituting for a, we get a = 15 and d = -2.
Therefore, the 3rd term is (a + 2d) = 11.
7. In an AP, the sum of the first 3 terms is -36 and that of the last 3 is 27. If there are 10 terms, what are the 1 st term and the common difference respectively?
A. 15, 3
B. -15, 3
C. 15, -3
D. -15, -3
Answer: B
Explanation:
The AP can be expressed as a, (a + d), ---, (a + 9d).
The sum of the first 3 terms is (3a + 3d) = -36 and the sum of the last 3 terms is (3a + 24d) = 27. Solving these two equations, we get a = -15 and d = 3.
8. In an AP, the sum of the first 3 terms is – 60 and that of the last 3 are 84. If there are 15 terms, what is the sum of the middle 3 terms?
A. 8
B. 12
C. 16
D. 24
Answer: B
Explanation:
Since the number of terms is odd, the AP can be expressed as (a – 7d), (a – 6d), ---, a, ---, (a + 6d), (a + 7d).
The sum of the first 3 terms is (3a – 18d) = -60 and the sum of the last 3 terms is (3a + 18d) = 84. Solving these two equations, we get a = 4 and d = 4.
Since the middle term is 4, the sum of the middle 3 terms is 12.
9. In an AP, the ratio of the 2nd term to the 6th term is 2/5. If the 8th term is 26, what is the 10th term?
A. 28
B. 29
C. 32
D. 33
Answer: C
Explanation:
The 2nd and the 6th terms are (a + d) and (a + 5d) respectively.
The ratio of these terms is 2/5. Solving this ratio, we get 3a = 5d.
The 8th term is (a + 7d) = 26. Substituting for a, we get a = 5 and d = 3.
Therefore, the 10th term is (a + 9d) = 32
10. The sum of the first 3 terms in an AP is 51 and that of the last 3 is 99. If the AP has 11 terms, what is the arithmetic mean of the middle 3 terms?
A. 17
B. 19
C. 21
D. 25
Answer: D
Explanation:
The AP can be expressed as a, (a + d), ---, (a +10d).
The sum of the first 3 terms is (3a + 3d) = 51 and that of the last 3 is (3a + 27d) = 99.
Solving these equations, we get a = 15 and d = 2.
The arithmetic mean of the 3 terms is the value of the middle term = 25.
11. Find the 5th term of the G. P.: 1/7,1/14, 1/28 ...
A. 1/108
B. 1/112
C. 1/128
D. 2/115
Answer: B
Explanation:

12. Find the sum of the following infinite G. P. 1/3, -2/9, 4/27, -8/81, ……
A. 1/2
B. 1
C. 1/3
D. 1/5
Answer: D
Explanation:
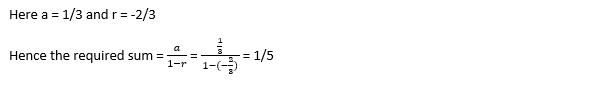
13. The distance travelled (in m) by a ball dropped from a height are 128/9, 32/3, 8, 6... How much distance will it travel before coming to rest?
A. 464/9 m
B. 120cm
C. 512/9 m
D. 256/9 m
Answer: C
Explanation:
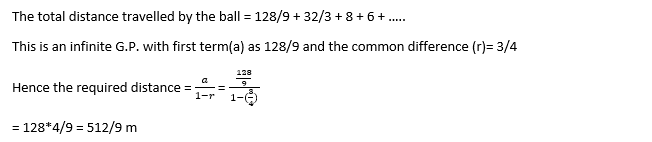
14. Find the G. M. between 4/9 and 169/9.
A. 26/3
B. 26/9
C. 15/9
D. 26/4
Answer: B
Explanation:
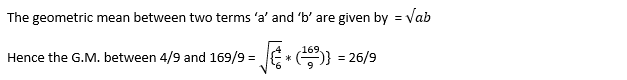
15. The arithmetic mean between two numbers is 75 and their geometric mean is 21. Find the numbers.
A. 133 and 17
B. 63 and 87
C. 3 and 147
D. 73 and 77
Answer: C
Explanation:

16. If the sum of reciprocals of first 11 terms of an HP series is 110, find the 6th term of HP.
1/5
1/10
2/7
1/20
Answer: B
Explanation:
The sum of first 11 terms of an AP = [2a + (11 – 1) d] 11/2 = 110
⇒ 2a + 10d = 20 ⇒ a + 5d = 10
Now there are 2 variables, but a + 5d = T6 in an AP series.
And reciprocal of 6th term of AP series will give the 6th term of corresponding HP series.
So, the 6th term of HP series is 1/10
17. Find the 4th and 8th term of the series 6, 4, 3, …
12/5 and 4/3
7/10 and 5/7
1/7 and 3/4
20/11 and 9/8
Answer: A
Explanation:
Consider 1/6, /14, 1/3, ...
Here T2 – T1 = T3 – T2 = 1/12
Therefore 1/6, 1/4, 1/3 is in A.P.
4th term of this Arithmetic Progression = 1/6 + 3 × 1/12 = 1/6 + 1/4 = 5/12,
Eighth term = 1/6 + 7 × 1/12 = 9/12.
Hence the 8th term of the H.P. = 12/9 = 4/3 and the 4th term = 12/5.
18. If the first two terms of a harmonic progression are 1/16 and 1/13, find the maximum partial sum?
1.63
1.13
1.89
2.2
Answer: A
Explanation:
The terms of the HP are 1/16, 1/13, 1/10, 1/7, 1/4, 1/-2, 1/-5
So, the maximum partial sum is 1/16 + 1/13 + 1/10 + 1/7 + 1/4 + 1/1 = 1.63
19. If the sixth term of an H.P. is 10 and the 11th term is 18 Find the 16th term.
30
75
90
80
Answer: C
Explanation:
Here a + 5d = 1/10
And a + 10d = 1/18
Solving these two equations, we get a = 13/90 and d = -2/225
We have a+15d = 13/90 – 2/15 = 1/90
Here the 16th term is 90.
20. An Arithmetic Progression has 23 terms, the sum of the middle three terms of this arithmetic progression is 720, and the sum of the last three terms of this Arithmetic Progression is 1320. What is the 18th term of this Arithmetic Progression?
A. 240
B. 360
C. 340
D. 440
Answer: B
Explanation:
The middle three terms of this Arithmetic Progression represent the eleventh, twelth & thirteenth term.
The average of these three terms will represent the twelth term
i.e., the 12th term will be 720/3 = 240.
The average of the last three terms will be the twenty second term i.e., 1320/3 = 440
The difference of twenty second term and the twelth term will give us ten times the difference i.e. 440 – 240 = 200/10 = 20 will be the difference.
If the twelth term is 240, the 18th term will be 240 + 6d i.e. 240 + 6 * 20 = 360 will be the 18th term. Therefore, 2nd option is the correct answer.
21. The first term of an AP is 10 and the last term is 28. If the sum of all terms is 190, what is the common difference?
A. 5
B. 3
C. 1
D. 2
Answer: D
Explanation:
The sum of all terms is (n/2) (a + l) = 190. This gives us n = 10.
The 10th term is (a + 9d) = 28. Substituting for a, we get d = 2
22. The sum of three numbers in an Arithmetic Progression is 45 and their product is 3000. What are the three numbers?
A. 5, 15, 25
B. 12, 15, 18
C. 10, 15, 20
D. -10, -15, -20
Answer: C
Explanation:
Assuming that the numbers are (a – d), a, (a + d) and their sum is 45
we get the middle number as 15.
Now, the product (a – d) (a + d) = 200. Solving, we get d = 5.
Therefore, the numbers are 10, 15 and 20
23. The sum of the first six terms of an AP is 48 and the common difference is 2. What is the 4th term?
A. 6
B. 7
C. 9
D. 10
Answer: C
Explanation:
The sum of six terms is 3 * (2a + 5 * 2) = 48.
Solving this, we get a = 3.
The 4th term is (a + 3d) = 9.
24. The sum of three numbers in Arithmetic Progression is 72 and their product is 11880. What are the numbers?
A. 21, 24, 27
B. 12, 24, 36
C. 18, 24, 30
D. 15, 24, 33
Answer: D
Explanation:
Assuming that the numbers in the Arithmetic Progression are (a – d), a, (a + d) and their sum is 72, we get the middle number as 24.
Now, the product (a – d) (a + d) = 495.
Solving, we get d = 9.
Therefore, the numbers are 15, 24 and 33.
25. The first term of an AP is 3 and the last term is 17. If the sum of all terms is 150, what is the 5th term?
A. 5
B. 7
C. 9
D. 11
Answer: B
Explanation:
The sum of all terms is (n/2)(a + l) = 150.
This gives us n = 15.
The 15th term is (a + 14d) = 17.
Substituting for a, we get d = 1.
Therefore, the 5th term is (a + 4d) = 7.