In this article, we will discuss the speed, time and distance aptitude questions. As this topic forms an integral part of every Entrance test as well as various competitive exams. Lets recall the Time, speed and Distance concept and formulas and apply them to solve variety of questions.
Formula's for Time Speed and Distance Questions
i. Distance = Speed × Time
ii. Speed = Distance/Time
iii. Time = Distance/speed
iv. 1(km/hr) = 5/18(m/s)
v. 1(m/s) = 18/5 (km/hr)
vi. If the ratio of the speeds of A and B is a:b then the ratio of times taken by them to cover the same distance is 1/a : 1/b or b:a.
vii. Average Speed= Total Distance/ Total Time
E.g.
A man goes First 30 km of his journey at the speed of 15km/hr , next 40km of this journey with 10km/hr and last 30 km of his journey with 30km/hr. Then calculate the average speed of the man.
Here Total distance is = 30km+40km+30km = 100km
We need to calculate Total time. Total Time= Time for 1st Part + Time of 2nd Part +Time of 3rd Part.
Time of 1st part = 30km /15 km/hr = 2 hrs
Time of 2nd part = 40km /10 km/hr = 4 hrs
Time of 3rd part = 30km /30 km/hr = 1 hr
Hence Total Time – 2+4+1 = 7 hours
Hence Average speed 100/7 km/hr
viii. If 2 objects are moving at the speed of Speed(1) and Speed(2) respectively for a certain distance then:
If the Distance is constant If time is constant
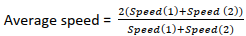
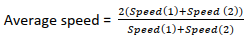
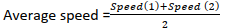
Relative Speed:
- If Two bodies are moving in opposite directions at speed S1& S2 respectively.
The relative speed is defined as Sr = S1 + S2
- Two bodies are moving in same directions at speed S1 & S2 respectively.
The relative speed is defined as Sr = |S1 − S2|
Top 10 Time Speed and Distance Questions
Q1) During the onward journey from Bombay to Pune, Deccan Queen travels at an average speed of 80 kmph, while on the return journey, the train is able to average a speed of 100 kmph. What is the average speed of the train on its entire journey?
A) 88(8/9)km/hr
B) 89(8/9)km/hr
C) 900/ 7
D) None
Solution :
Q2) Raju hikes up a hill at 4 mph and comes down at 6 mph. If the total time taken for the total journey is 3.5 hours, what was the distance between the hilltop and the foothills?
A) 9.4 miles.
B) 8.4 miles.
C) 84 miles
D) None
Solution :
Time taken = 3.5 hours both ways.
So, the two way distance = 4.8 x 3.5 miles = 16.8 miles.
Hence, the distance one-way = 8.4 miles.
Q3) A man travelled a distance of 61 km in 9 hours. He travelled partly on foot at 4 km/hr and partly on bicycle at 9 km/hr. What is the distance travelled on foot?
A) 14 km
B) 16 km
C) 18 km
D) 12 km
Solution :
Then the time in which he travelled on bicycle =(9−x) hr
distance = speed × time
⇒4x+9(9−x)=61
⇒4x+81−9x=61
⇒5x=20
⇒x=4
Q4) Walking 6/7th of his usual speed, a man is 12 minutes too late. What is the usual time taken by him to cover that distance?
A)1 hr 12 mins
B) 2 hr
C) 1 hr
D) 1 hr 42 mins
Solution :
Speed and time are inversely proportional.
Hence new time=7/6 of usual time
Hence, 7/6 of usual time - usual time =12 minutes
⇒1/6 of usual time =12 minutes
Therefore, usual time =12×6=72 minutes
=1 hour 12 minutes
Q5) The speed of a car increases by 2 kms after every one hour. If the distance travelling in the first one hour was 35 kms. what was the total distance travelled in 12 hours?
A) 456 kms
B) 552 kms
C) 482 kms
D) 556 kms
Solution :
This is an A.P with first term, a=35, number of terms,
n= 12,d=2.
Required distance = 12/2[2 x 35+{12-1) x 2]
=6(70+23)
= 552 kms
Q6) A thief is noticed by a policeman from a distance of 200 m. The thief starts running and the policeman chases him. The thief and the policeman run at the rate of 10 km and 11 km per hour respectively. What is the distance between them after 6 minutes?
A) 100 m
B) 150 m
C) 190 m
D) 200 m
Solution :
Distance covered in 6 minutes = (1/60) x 6 km = 1/10 km = 100 m
Therefore, Distance between the thief and policeman = (200 – 100) m = 100 m.
Q7) Two trains A and B start simultaneously in the opposite direction from two points P and Q and arrive at their destinations 16 and 9 hours respectively after their meeting each other. At what speed does the second train B travel if the first train travels at 120 km/h
A) 90 km/h
B) 160 km/h
C) 67.5 km/h
D) None of these
Solution :
⇒120s2=916=34
⇒s2=160km/h
Q8) Amy has to visit towns B and C in any order. The roads connecting these towns with her home are shown on the diagram. How many different routes can she take starting from A and returning to A, going through both B and C (but not more than once through each) and not travelling any road twice on the same trip?
A) 10
B) 6
C) 4
D) 8
Solution :
Clockwise, she has no choice of route from A to B, a choice of one out of two routes from B to C, and a choice of one out of two routes from C back to A. This gives four possible routes.
Similarly, anticlockwise she has four different routes.
Total routes = 8
Q9) A truck covers a distance of 376 km at a certain speed in 8 hours. How much time would a car take at an average speed which is 18 kmph more than that of the speed of the truck to cover a distance which is 14 km more than that travelled by the truck ?
A) 6 hours
B) 9 hours
C) 8 hours
D) 5 hours
Solution :
= 376/8 = 47 kmph
Now, speed of car = (speed of truck + 18) kmph
= (47 + 18) = 65 kmph
Distance travelled by car = 376 + 14 = 390 km
Time taken by car = Distance/Speed
= 390/65 = 6 hours.
Q10) In covering a distance of 30 km, Abhay takes 2 hours more than Sameer. If Abhay doubles his speed, then he would take 1 hour less than Sameer. Abhay's speed is:
A) 5 kmph
B) 6 kmph
C) 7.5 kmph
D) 6.25 kmph
Solution :
Then 30/x - 30/ 2x = 3
.6x = 30 x = 5 km/hrRelates Topics
